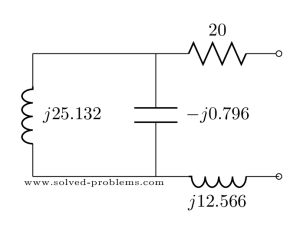
Determine the driving-point impedance of the network at a frequency of kHz:

Solution

Lets first find impedance of elements one by one:

Resistor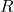

The resistor impedance is purely real and independent of frequency.

Inductors 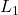and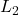

The inductor impedance is purely imaginary and directly proportional to frequency:

We need to find the impedance in kHz. Therefore:

Capacitor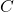

The capacitor impedance is purely imaginary and inversely proportional to frequency:

To get the standard representation of complex numbers, we need to bring to numerator and this can be done by multiplying by :

Note how capacitor acts in this frequency. The value of impedance is less than . Compare this value to values of other components. It is almost equivalent to a short circuit!

Equivalent Impedance

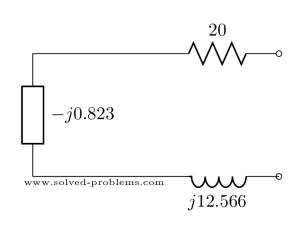
Let’s replace the values in the circuit:

and are parallel.

One interesting point here is that unlike pure resistive circuits where the equivalent resistance of parallel elements is always less than the resistance of each element, the value of the equivalent impedance of parallel elements can be greater than the value of the impedance of elements. Here the capacitor impedance value is but the equivalent impedance, , is higher.

Three components are in series. Therefore:

Now, determine the impedance at Hz and kHz and share it with others below in comments section.