A quadratic equation can be solved by taking the square root of both sides of the equation. This method uses the square root property,
![]()
Before taking the square root, the equation must be arranged with the x2 term isolated on the left- hand side of the equation and its coefficient reduced to 1. There are four steps in solving quadratic equations by this method:
Step 1: Isolate the ![]() and
and ![]() terms. Use the addition and subtraction and isolate the
terms. Use the addition and subtraction and isolate the ![]() and
and ![]() terms on the left-hand side of the equation. Then, use the multiplication and division axioms to eliminate the coefficient from the
terms on the left-hand side of the equation. Then, use the multiplication and division axioms to eliminate the coefficient from the ![]() term.
term.
Step 2: Make the coefficient on the ![]() term equal to
term equal to ![]() . Use multiplication or division to eliminate the coefficient from the
. Use multiplication or division to eliminate the coefficient from the ![]() term.
term.
Step 3: Complete the square. To complete the square, take the coefficient of the ![]() term, square it, and divide it by 4.
term, square it, and divide it by 4.
Step 4: Solve the equation in step 3 by taking the square root of both sides of the equation.
Example 1: ![]()
Step 1: Isolate the ![]() and
and ![]() terms.
terms.
![]()
Step 2: Make the coefficient on the ![]() term equal to
term equal to ![]() .\\
.\\
It is already ![]() .
.
Step 3: Complete the square.
![]()
![]()
Step 4: Solve the equation in step 3 by taking the square root of both sides of the equation.
![]()
Example 2: ![]()
Step 1: Isolate the ![]() and
and ![]() terms.
terms.
![]()
Step 2: Make the coefficient on the ![]() term equal to
term equal to ![]() .\\
.\\
It is already ![]() .
.
Step 3: Complete the square.
![]()
![]()
Step 4: Solve the equation in step 3 by taking the square root of both sides of the equation.
![]()
Example 3: ![]()
Step 1: Isolate the ![]() and
and ![]() terms.
terms.
![]()
Step 2: Make the coefficient on the ![]() term equal to
term equal to ![]() .\\
.\\
![]()
Step 3: Complete the square.
![]()
![]()
Step 4: Solve the equation in step 3 by taking the square root of both sides of the equation.
![]()
Example 4: ![]()
Step 1: Isolate the ![]() and
and ![]() terms.
terms.
![]()
Step 2: Make the coefficient on the ![]() term equal to
term equal to ![]() .\\
.\\
![]()
Step 3: Complete the square.
![]()
![]()
Step 4: Solve the equation in step 3 by taking the square root of both sides of the equation.
![]()
I’m confused about step 3 in example 1. You’ve added 16 to both sides, which I assume you got from squaring the coefficient of the x term, 4. But shouldn’t you then divide 16 by 4, so that you add 4 to both sides? I don’t understand how (x + 4)^2 is the same as x^2 + 4x + 16.
Hi Rob,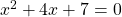 to
to 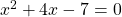 (just to have real answers)
(just to have real answers)
I apologize, my solution was wrong. I also changed the problem from