Determine the power of ![]() and
and ![]() . (Hint: there is no need to use nodal analysis; voltages between nodes can be easily found by the voltage sources.)
. (Hint: there is no need to use nodal analysis; voltages between nodes can be easily found by the voltage sources.)
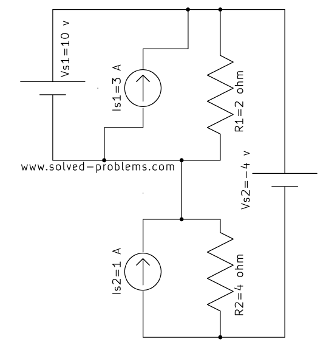
Solution
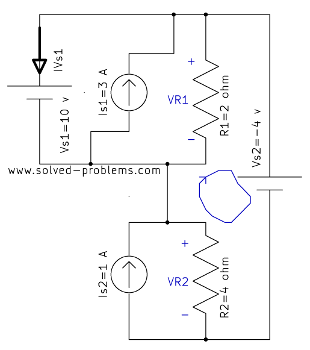
![]()
KVL around the loop shown above:
![]() . Therefore,
. Therefore, ![]()
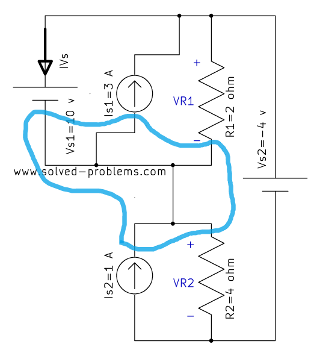
KCL at the node shown in the figure:
![]()
![]() , absorbing.
, absorbing.
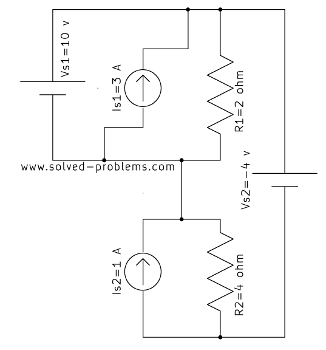
You made a mistake in calculating VR2. It should be -6v.