Nodal Analysis – Circuit with Dependent Voltage Source

Determine the power of each source after solving the circuit by the nodal analysis.

Answers: $P_{I_x}=0.497W, P_{1A}=-1.806W, P_{2A}=4.254W, P_{3V}=-3.87W,$ and $P_{5V}=-3.552W$

Solution

I. Identify all nodes in the circuit.
The circuit has 6 nodes as highlighted below.

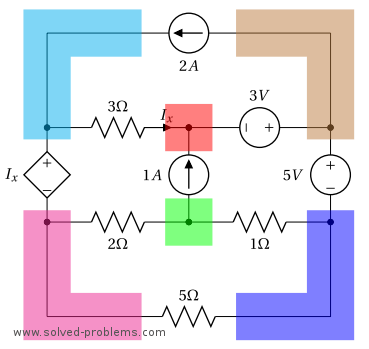
II. Select a reference node. Label it with the reference (ground) symbol.

The right top node is connected to two voltage sources and has three elements. All other nodes also have three elements. Hence, we select the right top node because by this selection, we already know the node voltages of two other nodes, i.e. the ones that the reference node is connected to them by voltage sources.

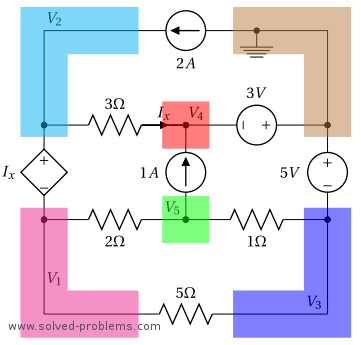
III. Assign a variable for each node whose voltage is unknown.
We label the remaining nodes as shown above. Nodes of $V_3$ and $V_4$ are connected to the reference node through voltage sources. Therefore, $V_3$ and $V_4$ can be found easily by the voltages of the voltage sources. For $V_3$ , the negative terminal of the voltage source is connected to the node. Thus, $V_3$ is equal to minus the source voltage, $V_3=-5 V$ . The same argument applies to $V_4$ and $V_4=-3V$ .

IV. If there are dependent sources in the circuit, write down equations that express their values in terms of node voltages.

The voltage of the dependent voltage source is $I_x$ . We should find this value in terms of the node voltages. $I_x$ is the current of the $3\Omega$ – resistor. The voltage across the resistor is $V_2-V_4$ . We prefer to define $V_{3\Omega}$ as $V_2-V_4$ instead of $V_4-V_2$ to comply with passive sign convention. By defining $V_{3\Omega}$ as mentioned, $I_x$ is entering from the positive terminal of $V_{3\Omega}$ and we have $V_{3\Omega}= 3 \Omega \times I_x$ . Therefore, $I_x=\frac{V_2-V_4}{3\Omega}$ . $\to I_x=\frac{V_2}{3} +1$

V. Write down a KCL equation for each node.

Nodes of $V_1$ and $V_2$ :
These two nodes are connected through a voltage source. Therefore, they form a supernode and we can write the voltage of one in terms of the voltage of the other one. Please note that the voltage of the dependent voltage source is $I_x$ and we have $V_2=V_1+I_x$
$\to V_2=V_1+\frac{V_2}{3} +1 \to \frac{2}{3} V_2=V_1+1$
$\to V_1=\frac{2}{3} V_2-1$

KCL for the supernode:
$\frac{V_1-V_3}{5\Omega}+\frac{V_1-V_5}{2\Omega}+\frac{V_2-V_4}{3\Omega}-2A=0$
$\to \frac{V_1+5}{5}+\frac{V_1-V_5}{2}+\frac{V_2+3}{3}-2=0$
$\to \frac{V_1}{5}+\frac{V_1-V_5}{2}+\frac{V_2}{3}=0$
$\to 21V_1-15V_5+10V_2=0$
Substituting $V_1=\frac{2}{3} V_2-1$ ,
$\to 8V_2-5V_5=7$

Node of $V_5$ :
$\frac{V_5-V_1}{2 \Omega} +\frac{V_5-V_3}{1 \Omega}+1=0$
$\to -V_1 +3V_5-2V_3+2=0$
Substituting $V_1=\frac{2}{3} V_2-1$ and $V_3=-5 V$ ,
$\to -2 V_2 +9V_5=-39$

Here is the system of equations that we need to solve and obtain $V_2$ nd $V_5$ :

$\left\{ \begin{array}{l} I: 8V_2-5V_5=7 \\ II: -2 V_2 +9V_5=-39 \end{array} \right.$

We use elimination method to solve this system of equation:
$(II)\times 4 +(I): 31V_5=-149 \to$
$V_5=-4.806 V$
$V_2=\frac{9V_5+39}{2} \to$
$V_2=-2.127 V$
Using $V_1=\frac{2}{3} V_2-1$ ,
$V_1=-2.418 V$

All node voltages are determined. Now, the power of voltage sources can be calculated from the node voltages. For each source, we need to find the voltage across the source as well as the current flowing through it to compute the power.

$2A$ current source:
The voltage across the $2A$ current source is equal to $V_2$ . However, the comply with the passive voltage convention, the current should be entering from the positive terminal of the defined voltage as shown below. Therefore, $V_{2A}=-V_2=2.127 V$ .

$P_{2A}=2A \times V_{2A}=4.254W$ absorbing power

$1A$ current source:

To compliant with the passive sign convention, the voltage $V_{1A}$ should be defined with polarity as indicated above. We have $V_{1A}= V_5-V_4=-1.806V$ . Hence,

$P_{1A}=1A \times (-1.806 V)=-1.806W$ supplying power.

$5V$ voltage source:

$I_{5V}$ should be defined such that it enters from the positive terminal of the source in order to use the voltage of the source in power calculation. Another option is to use $V_3$ and define the current as entering from the voltage source terminal connected to the node of $V_3$ . We use the first approach here. KCL should be applied in the node of $V_3$ to determine $I_{5V}$ .

KCL @ Node of $V_3$ :

$-I_{5V}+I_{1\Omega}+I_{5\Omega}=0$
$\to I_{5V}=\frac{V_3-V_5}{1\Omega}+\frac{V_3-V_1}{5\Omega}=-0.7104A$

$P_{5V}=5V \times (-0.7104 A)= -3.552 W$ supplying power.

$3V$ voltage source:

Likewise, $I_{3V}$ should be defined as shown above to comply with the passive sign convention. We apply KCL to the reference node to find $I_{3V}$ .

KCL @ the reference node:

$I_{5V}+I_{3V}+2A=0$
$\to I_{3V}=-1.29A$

$P_{3V}=3V \times (-1.29 A)= -3.87 W$ supplying power.

The dependent source:
The voltage of the dependent source is $I_x$ and we define its current $I_{I_x}$ with the direction illustrated above. $I_{I_x}$ can be calculated by applying KCL at the node of $V_2$ . The current of the $3\Omega$ resistor is $I_x$ which is equal to $\frac{V_2}{3} +1= 0.291A$ .

KCL @ Node of $V_2$ :

$-2A+I_x+I_{I_x}=0 \to I_{I_x}=1.709A$

$P_{I_x}=I_x \times I_{I_x}=0.291 V \times 1.709 A= 0.497W$ absorbing power.

The PSpice simulation result is shown below. The PSpice schematics can be downloaded from http://www.solved-problems.com/download/1-23.zip.

Join the Conversation

8 Comments

kirchhoff says:

October 6, 2010 at 12:07 pm

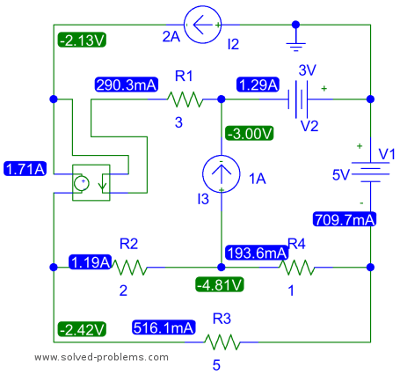
There was a faster method to solving the network ! 😉

1. Dr. Yaz Z. Li says:
  
  October 6, 2010 at 5:49 pm
  
  Mesh analysis is easier because there are only 4 meshes. However, it is required to be solved with the nodal analysis. I would appreciate it if you share your solution with us. Thanks.
  
ddzolt says:

October 8, 2010 at 8:17 pm

Mesh analysis is better (only two mesh not four), but ther’s another faster way.

But how can I post my solution ?

1. Dr. Yaz Z. Li says:
  
  October 8, 2010 at 10:16 pm
  
  I upgrade your membership. You should be able to create a new post from here (after login). Please write your solution there. I will somehow attach it here.
  To see how to write a post , watch this.
  Thanks.
  
knowledge seeker says:

August 13, 2011 at 1:15 pm

awesome work

alex says:

October 18, 2011 at 6:01 am

Hey guys thanx for sharing ur knowledge. the example really helped me. i am currently taking this course in college and i am struggling. this example was more helpful than what the professor has been teaching. what are your tips to find more motivation to help me succeed in this course??

natural back pain relief dr oz says:

June 19, 2013 at 9:09 am

Good info. Lucky me I discovered your blog by accident
(stumbleupon). I have book-marked it for later!

Joya says:

August 7, 2015 at 2:04 pm

i have some problems regarding nodal analysis and mess.
how can I post the question here?

Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Nodal Analysis – Circuit with Dependent Voltage Source

Published by Yaz

Join the Conversation

Leave a comment

Cancel reply